For a complete list of Beginners articles, see Financial Crisis for Beginners.
I’ve had two posts so far on the terms under which Treasury sold back to Old National the warrants on Old National stock that Treasury got in exchange for its TARP investment, so I thought it was time for an introduction to warrant/option pricing.
The warrants received by Treasury give Treasury the right to buy common stock in the issuing bank under predefined terms. Buying the stock is called exercising the warrant. The warrant specifies how many shares Treasury can buy; the price that it must pay to buy them (the exercise price); and the term of the warrant, meaning how long Treasury has to decide whether or not it wants to exercise the warrant. If Treasury never exercises the warrant, then it expires and nothing happens. For our purposes, a warrant is the same as a call option; there are some differences I will ignore, which are outlined here.
Warrant terms
These warrants were part of the terms of the TARP Capital Purchase Program, which is what Treasury used to recapitalize banks last fall, starting in October. The warrants have value for Treasury – how much, I’ll get into later. Therefore, they make it possible for Treasury to be more generous with other terms of the transaction. Arguably, the warrants helped compensate for the fact that Treasury was buying preferred stock with a very low dividend yield – only 5%. There is no way that most banks would have been able to issue new preferred stock with only 5% dividends back in October-November. Probably the more important reason the warrants were mixed in was that they made it easier to justify the transaction politically; through the warrants, the taxpayer could “participate in the upside” if things went well, because if the stock price went up, the warrants would become more valuable.
As part of the Capital Purchase Program, banks had to give Treasury warrants on common stock equal in value to 15% of the amount of money invested. Treasury invested $100 million in Old National, so it needed warrants on $15 million worth of common stock. So it got warrants to buy 813,008 shares at an exercise price of $18.45; 813,008 * 18.45 = 15 million, or something very close to it. $18.45 represented the value of the common shares at the time of the investment. The idea is that the warrants were supposed to be “at the money;” if the stock went up, Treasury could exercise the warrants and make money; but if it went down, Treasury would get nothing (at least not from exercising the warrants).
Actually, that isn’t quite accurate, for two reasons. First, according to the original term sheet, the exercise price was set not at the share price on the investment date itself, but as the average of the closing price for the twenty previous trading days; the idea here, which is common, is to protect both sides against day-to-day swings in stock prices. In Old National’s case, that would have been $16.35. However, in early April the Wall Street Journal reported that Treasury changed the terms to base the exercise price on the date that the bank’s application to participate in the CPP was approved, which was an earlier date. Because November-December was a period of falling bank stock prices, in the large majority of cases the change in dating had the effect of increasing the exercise price of the warrants, thereby reducing the value of the warrants to Treasury (because it would have to pay more for each share). In Old National’s case, it produced an exercise price of $18.45 instead of $16.35.
(Ilya Podolyako actually drafted a post about this at the time, but I chose not to publish it because I didn’t want to be hammering Treasury for every little thing they did that helped the banks. But I think it’s an important part of this story. Ilya also pointed out that when private companies do this kind of thing – setting the exercise price based on market prices in the past – it’s called backdating, and it’s illegal. My apologies to Ilya for not publishing the post then.)
Those warrants have a term of 10 years, meaning that Treasury has until 2018 to decide whether or not to exercise them. They also have an unusual “Reduction” feature, which says that if the bank raises more money than Treasury invested by the end of 2009, through sales of new common or perpetual preferred stock, half of the warrants will instantly evaporate.
Warrant pricing
So how much are these things worth? On the date of the sale, Old National’s common shares were trading at $14.70 – $3.75 below the exercise price of the warrants. So if Treasury had done the crazy thing and exercised the warrants, it would have paid $18.45 for a share of stock worth $14.70, for a total loss of about $3 million.
However, the warrants themselves, like all options, always have some positive value, as long the term has not expired. You never have to exercise the warrants, so in no scenario will you be forced to lose money on them; and there is always some chance that the stock price will go above the exercise price, at which point you could exercise them and make money. The question is how much.
Conceptually speaking, you are trying to figure out the chances that the stock will someday be worth more than $18.45, times the profit you will make from exercising the warrants at that point. This clearly depends on the following parameters:
- Exercise price: The higher the exercise price, the less likely your warrant is to make you money.
- Current stock price: The higher the current price, the more likely you are to make money.
- Time to maturity: The more time you have, the higher the chances that the stock price will climb above the exercise price.
And it depends on one more parameter: volatility or, roughly speaking, the tendency of the stock price to move up and down. In the case of Old National, the stock price has to go up by $3.75 (25.5%) before the warrant can be exercised at a profit; the more volatile the stock, the more likely this is.
Making some additional assumptions, like zero transaction costs and zero dividends, Fischer Black and Myron Scholes worked out a formula to calculate the value of an option from these parameters (and the risk-free interest rate, since you are looking at the future and money loses value over time), which is now known as the Black-Scholes formula, and has been described as the central pillar, for better or worse, of modern finance. (Nassim Taleb strongly disagrees.) I think I had to derive the formula in a micro class a long time ago, but my memory of that year is a bit fuzzy, perhaps because I met my wife in that class.
In any case, the formula incorporates this useful intuition: To calculate the value of an option, you only need to know the expected value of exercise on the maturity date. This is because, theoretically, that is the only day on which you should ever exercise an option. Even if your option is $10 “in the money” (market price exceeds exercise price by $10), there is always a little bit of extra option value, because the potential upside is infinite, and the potential downside is bounded by $10.
Note that the formula says you can price an option without even having an opinion about the fundamental value of the underlying stock – all you need are its current price and its volatility. This is consistent with a general (though not necessarily correct) principle that stock markets always efficiently price assets, so any opinion you may have about the stock’s fundamental value is foolish.
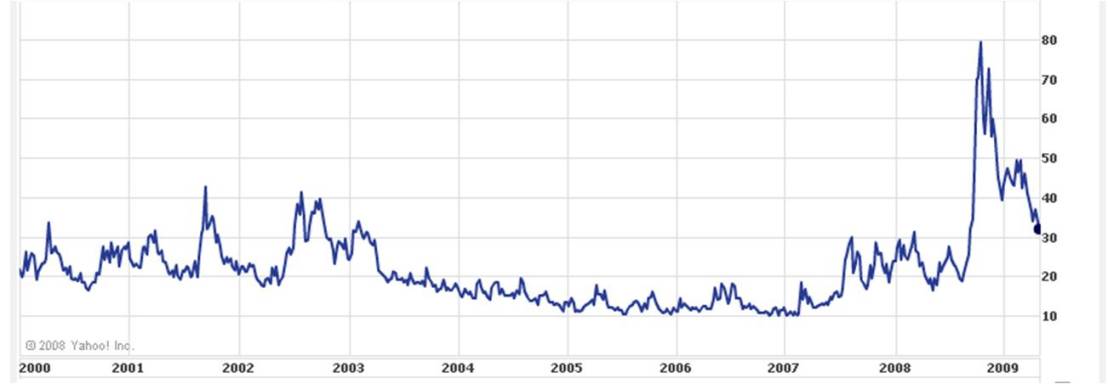
Also note that the key assumption in the formula is that stock prices will move randomly with constant volatility, and the key parameter in the formula is volatility. The other inputs are basically observable (though not quite in the case of the risk-free rate), but volatility is not. You need to know the volatility of the stock price between now and the maturity date, but all you can see is its volatility in the past. This makes option pricing especially difficult right now, because stock price volatility has been much higher over the last eight months than over the previous eight years. (The chart is the implied volatility of the S&P 500 since 2000.)
So if you use the volatility over the last eight months, you will get a much higher warrant value than if you use the volatility over the last eight years. More fundamentally, using any volatility assumption based on past data falls into the trap of assuming that the future will be like the past. This is never a foolproof assumption, and the longer the timeframe you are looking at, the worse the assumption becomes. It usually may not matter a lot for typical short-dated options (30 days, 60 days, etc.) – unless the world changes during those 30 days – but it matters a lot for long-dated warrants, like the 10-year warrants that Treasury got.
Real stocks also pay dividends, and the higher the future dividends, the less your warrant will be worth – because those dividends essentially come out of the future stock price. So your formula has to have some estimate of what dividend payouts will be. Again, this is especially hard right now, because many banks – including Old National – have drastically cut their dividends recently, and it’s difficult to predict when they will go back to paying higher dividends.
Finally, the “Reduction” feature of the TARP warrants throws another wrench into the works. To value the warrants, you have to take into account the fact that half of them could vanish if Old National raises $100 million by issuing stock before the end of the year; and as long as the warrants were outstanding, they had an incentive to raise that money. That involves making guesses about the overall funding climate, and the corporate strategy of Old National, neither of which can be statistically estimated.
So now you should know enough to understand the three key assumptions behind the estimates in Linus Wilson’s paper. (However, the Bloomberg story does not provide its option pricing assumptions.) You should also be able to follow the discussion over assumptions between q and Sandrew in the comments to my previous post, beginning here.
What should Treasury have done?
q, a regular commenter here, concludes that the price Treasury got is within the range of reasonableness, given his preferred set of assumptions. However, he also says (agreeing with Nemo) that Treasury should not have negotiated a sale to Old National, but should have simply held onto them until maturity (remember, you don’t want to exercise them early); if the real issue was restrictions placed on TARP money, the government could have rolled them back (for banks that bought back their preferred shares). Or, if Treasury didn’t want to hold onto them, they could have auctioned them off.
While these are economically superior to simply negotiating a sale in a market with a single potential buyer (Old National), it gets us into the complicated world of TARP terms and conditions. First, the original term sheet said that Treasury could not sell more than 50% of the warrants before the end of 2009, because, remember, 50% of the warrants would vanish if the bank made a qualifying equity offering. Still, Treasury could have sold half and then held the rest; this would have had the salutary effect of giving Old National an incentive to raise new capital.
Second, assuming Treasury did not sell the warrants, when Old National bought back its preferred shares, it got the right to buy back the warrants at “fair market value” – but there is no market. (You can get a quote on short-dated options, but not long-dated ones – these are typically over-the-counter.) I haven’t found the implementation rules, but an article in Fortune said this:
February’s stimulus legislation – which gave TARP recipients the right to repay funds without raising new capital or observing any waiting period – specified that Treasury must liquidate a bank’s warrants at the current market price after it repays its TARP preferred stock.
I gather from bits and pieces I remember reading that there is some sort of appraisal process where the bank and Treasury first try to agree on a value, and I believe if that fails then there is supposed to be an auction. Auction participants would know all about option pricing, of course, and would apply a range of assumptions; presumably the sale would go to the buyer with the highest volatility assumption, which would probably (but not certainly) yield a higher price than Treasury got.
Of course, the banks have their opinion about all this (from the same Fortune article):
The American Bankers Association trade group last week sent Treasury Secretary Tim Geithner a letter calling for the government to eliminate the warrant-repayment provision altogether. The ABA said repurchasing the warrants amounts to an “onerous exit fee” for banks that have already repaid in full the funds they got from Treasury. . . .
Treasury must attempt to liquidate the warrant, the stimulus legislation says. But the ABA decries this as well, saying in its letter that selling the warrant to a third party could unfairly dilute a bank’s shareholders.
In other words, Treasury should just rip up the warrants – even though the warrants were one reason why the banks got investments on such generous terms in the first place. How times have changed since last fall.
By James Kwak
Second, assuming Treasury did not sell the warrants, when Old National bought back its preferred shares, it got the right to buy back the warrants at “fair market value” – but there is no market. (You can get a quote on short-dated options, but not long-dated ones – these are typically over-the-counter.)
I gather from bits and pieces I remember reading that there is some sort of appraisal process where the bank and Treasury first try to agree on a value, and I believe if that fails then there is supposed to be an auction.
It’s funny how much this paper transaction extemporizing (here the warrants, usually the toxic assets), all trying to maintain the charade of a capitalist “market” where none exists on order to prop up these unviable banks, is redolent of childern pretending to play a game but lacking some of the requisite equipment and just improvising (and improvising the rules as well).
Of course, the banks have their opinion about all this (from the same Fortune article):
The American Bankers Association trade group last week sent Treasury Secretary Tim Geithner a letter calling for the government to eliminate the warrant-repayment provision altogether. The ABA said repurchasing the warrants amounts to an “onerous exit fee” for banks that have already repaid in full the funds they got from Treasury. . . .
Treasury must attempt to liquidate the warrant, the stimulus legislation says. But the ABA decries this as well, saying in its letter that selling the warrant to a third party could unfairly dilute a bank’s shareholders.
In other words, Treasury should just rip up the warrants – even though the warrants were one reason why the banks got investments on such generous terms in the first place. How times have changed since last fall.
Of course no one should have expected the underlying attitudes of the bankers to change. They have always believed and will always believe for as long as they’re allowed to do so that society exists only as a resource for them to mine.
And they absolutely believe society should be grateful for the privilege of serving as this resource.
So it’s not surprising that, since the nominal change in administrations (and what should have been a change in Congress starting in 2007) brought no Change at all where it came to government ideology vis the FIRE sector, “times have changed” in how emboldened the bankers feel in more openly displaying their lack of remorse, their own sense of entitlement and aggrievement, and their ruthless will to continue and intensify their feudal practices.
As Rehoboam said to the supplicants who had hoped he’d spare his father’s whip: “I will chastise you not with whips but with scorpions”.
So none of that’s surprising, given the lack of political Change. What is somewhat surprising, despicably so, is this absolute lack of change, coming from an someone whose fundamental campaign promise was “Change”.
This will be justified by the banks claiming that the warrants were issued as some sort of collateral for a loan, and now that the loan is repaid, there is no further need for the collateral. And your average taxpayer will believe that, as he won’t understand how this works.
An interesting article from the Barron’s option specialist, gives some estimates of the values of various banks’ warrants held by the US:
http://online.barrons.com/article/SB124303102707848333.html
An excerpt:
Based on this methodology, Citigroup’s warrants were worth about $166 million on May 20, down from $1.67 billion when issued Oct. 28; Bank of America’s warrants were worth about $221 million, versus $921 million; and Wells Fargo’s, about $1.06 billion, down from $1.48 billion.
On the other hand, this method showed that Uncle Sam has made money on the warrants issued to Goldman, Morgan Stanley and JPMorgan. Goldman’s warrants were calculated to be worth $982 million on May 20, up from $680 million; JPMorgan’s, $1.4 billion, up from $1.2 billion; Morgan Stanley’s, $1.25 billion, versus $410 million. The combined value of those three rose from about $2.3 billion on Oct. 28 to about $3.7 billion, producing a gain of $1.4 billion.
If I remember correctly, the warrants provisions weren’t in the earliest TARP plan, and were inserted later to insure against the government substantially overpaying for the toxic securities that most people assumed it would be buying within days of passage. In other words, they were based on the idea that there we were going to have a program where the government would quickly relieve the banks of their troubled assets – that’s why we called it “TARP”.
The problem, of course, is that no one knew what these things were worth (apparently, we still don’t, and almost 8 months later). If the government bought them early on with overly optimistic assumptions and a rosy baseline scenario – the banks would not merely have been saved – they could have made a killing on worthless securities, with the entire loss distributed to the public.
The warrants were supposed to insure that there would be a mechanism whereby any “undue” gain on the part of the financial institutions, which, presumptively, would be reflected in their share prices over the long term, could be easily recouped by the taxpayer.
But the Treasury didn’t buy the assets from the banks when it recapitalized them, and months later we have yet to remove them through the flawed PPIP apparatus. The evaporation clause might have sensibly extinguished 100% of the warrants “in the event we confuse the entire congress as to what they are doing and don’t actually buy your junk.”
So, since the warrants do not serve their original risk-management purpose, it doesn’t seem unreasonable to me to allow healthy institutions that are willing to fend for themselves to opt-out of government control by paying back every dime they borrowed with interest. The taxpayer has lost nothing on the deal.
as mr. kwak says, i think the treasury got a plausibly reasonable deal here. i say this, obviously, without knowing what kind of deal it could have got auctioning the warrants.
the model price of long dated warrants depends a lot on your assumptions, and i am choosing assumptions that i think are reasonable here.
i assume a volatility of 25%, and i think this is not a low estimate. my rationale for this is that 100-day volatility for ONB averaged 18% and never went above 27%.
i assume a dividend yield of 3.83 which is the historical dividend yield and which is Wilson’s middle number.
i assume a 30% probability of a stock offering, but note that this offering has a higher probability than a fair sale of these warrants on the open market. i think the treasury would assume a higher probability, perhaps 100%.
i assume a borrow rate of 0.50%. this is a proxy for ‘hedging cost’ or ‘risk premium’ as most private investors would hedge these options (which costs money) or expect a higher expected return from this investment than what they can get for treasury bonds. this 0.50% is added to dividend yield.
the number i get is $1.83 per warrant, or $1.26M.
here is a link to my calculation (ht Sandrew on pointing out that wolfram alpha is capable of this)
http://www78.wolframalpha.com/input/?i=option&a=*C.option-_*Formula.dflt-&a=*FP.FinancialOption.OptionName-_VanillaEuropean&a=*FP.FinancialOption.OptionType-_Call&f4=18.45&f=FinancialOption.StrikePrice_18.45&f5=9.65+years&f=FinancialOption.TimeToExpiration_9.65+years&f6=14.7&f=FinancialOption.UnderlyingPrice_14.7&f7=25%25&f=FinancialOption.Volatility_25%25&f8=4.43&f=FinancialOption.DividendYield_4.43&f9=3.19%25&f=FinancialOption.RiskFreeInterestRate_3.19%25&a=*FVarOpt.1-_***FinancialOption.TimeToExpiration–.***FinancialOption.ExpirationDate-.*FinancialOption.CurrentDate—.*–
There were several inaccuracies in James’ option pricing primer, so for those planning on using it, please see the observations below:
As part of the Capital Purchase Program, banks had to give Treasury warrants on common stock equal in value to 15% of the amount of money invested. Treasury invested $100 million in Old National, so it needed warrants on $15 million worth of common stock. So it got warrants to buy 813,008 shares at an exercise price of $18.45; 813,008 * 18.45 = 15 million, or something very close to it. $18.45 represented the value of the common shares at the time of the investment.
[The math is wrong – the author derived the exercise value not the market value.]
(Ilya Podolyako actually drafted a post about this at the time, but I chose not to publish it because I didn’t want to be hammering Treasury for every little thing they did that helped the banks.
[This bit is editorial – Helped yes, by setting a higher strike, the banks’ liability to the Treasury was reduced – but a reasonable argument might be made that the terms under which the warrants were originally issued were made under duress.]
Making some additional assumptions, like zero transaction costs and zero dividends, Fischer Black and Myron Scholes worked out a formula to calculate the value of an option from these parameters (and the risk-free interest rate, since you are looking at the future and money loses value over time), which is now known as the Black-Scholes formula, and has been described as the central pillar, for better or worse, of modern finance. (Nassim Taleb strongly disagrees.)
[This is background – Nassim does not want Black or Scholes names associated with option pricing, because they didn’t invent the math, they just figured out how to apply the heat transfer equation to option pricing. By the same logic, the Gaussian (or normal) distribution, should be called the de Moivre distribution. Nassim has some issues.]
In any case, the formula incorporates this useful intuition: To calculate the value of an option, you only need to know the expected value of exercise on the maturity date. This is because, theoretically, that is the only day on which you should ever exercise an option.
[I think these options may be exercised by Treasury before the maturity (called American-style), and thus this statement is incorrect – the boundary condition (essentially, a sell-vs.-hold rule) defining the exercise region must be evaluated at all points in time up to expiration.]
Note that the formula says you can price an option without even having an opinion about the fundamental value of the underlying stock – all you need are its current price and its volatility. This is consistent with a general (though not necessarily correct) principle that stock markets always efficiently price assets,
[This is incorrect in a couple of ways. First, Black-Scholes is “arbitrage-free”, so it only requires that the dynamics of the underlying follows geometric Brownian motion – it imposes no requirements on the stock price in relation to fundamental falue. Second, I am pretty confident that my memory is correct that Mark Rubinstein and John Cox had a very cute extension to Black-Scholes in their book Option Pricing from 1979 that included the impact of a subjective evaluation of stock price.]
Also note that the key assumption in the formula is that stock prices will move randomly
[Randomly, in the sense of geometric Brownian motion with drift – so e.g., no discontinuous jumps allowed.]
with constant volatility
[actually with deterministic, not constant volatility – the volatility can be non-constant, just needs to be a deterministic function of time (as long as we are sticking with Black-Scholes, that is).]
You need to know the volatility of the stock price between now and the maturity date, but all you can see is its volatility in the past. This makes option pricing especially difficult right now, because stock price volatility has been much higher over the last eight months than over the previous eight years. (The chart is the implied volatility of the S&P 500 since 2000.)
[The author seems a bit confused about what implied volatility is, or he was not careful in his choice of words. Of course, implied vol is usually interpreted as the market’s expectation of future volatility. So this chart is actually a movie of the market’s forward looking evaluation of volatility, as it changed over this period of time.]
More fundamentally, using any volatility assumption based on past data falls into the trap of assuming that the future will be like the past. This is never a foolproof assumption, and the longer the timeframe you are looking at, the worse the assumption becomes. It usually may not matter a lot for typical short-dated options (30 days, 60 days, etc.) – unless the world changes during those 30 days – but it matters a lot for long-dated warrants, like the 10-year warrants that Treasury got.
[Probably the author’s confusion about what is implied vol versus historical vol prevented him from suggesting that we take the vol surface for the Bank’s options at the date we are interested in valuation of the warrants and extrapolate from that forward looking information as necessary to get to the ten year point – a caveat is in order, though, as extrapolation is a very bad thing ordinarily, because the errors are going to be huge in all likelihood.]
Finally, the “Reduction” feature of the TARP warrants throws another wrench into the works. To value the warrants, you have to take into account the fact that half of them could vanish if Old National raises $100 million by issuing stock before the end of the year; and as long as the warrants were outstanding, they had an incentive to raise that money. That involves making guesses about the overall funding climate, and the corporate strategy of Old National, neither of which can be statistically estimated.
[The value per unit is not a function of the “Reduction” feature. The total value is a function of the number of units that are to be sold, of course. It is possible the author is referring to an aspect of warrant valuation that he specifically excluded from the discussion above, specifically that warrants, because they create new shares when exercised, dilute the share price. As a result, their value needs to be adjusted downward for this dilution effect – which problem has been solved a long time ago, and the conditions are easier here, because unlike the general problem of warrant exercise, there is no competitive strategic element to deciding the optimal exercise time (no game to be played against other warrant holders, about who gets less diluted shares by exercising slightly earlier).]
q, a regular commenter here, concludes that the price Treasury got is within the range of reasonableness, given his preferred set of assumptions. However, he also says (agreeing with Nemo) that Treasury should not have negotiated a sale to Old National, but should have simply held onto them until maturity (remember, you don’t want to exercise them early);
[Two things wrong here. First, remember, you may want to exercise them early, if they are American-style, and I think they are. Second, a sale is not an exercise – you will always be willing to sell an option American or any other exercise type, for a fair price (since the fair price incorporates the “premium” for not waiting till expiration). Opinion to follow – The only two reasons for the Treasury not to sell are (1) they couldn’t agree a fair price or (2) they want to keep their claws in the bank as long as possible.]
Second, assuming Treasury did not sell the warrants, when Old National bought back its preferred shares, it got the right to buy back the warrants at “fair market value” – but there is no market. (You can get a quote on short-dated options, but not long-dated ones – these are typically over-the-counter.
[Not sure if the author is using accounting-ese here, and saying that because these would be Level III assets, there is no fair value. That is just accounting-ese, however. The fair value is what price the parties _freely_ agree to exchange them for. Don’t know, maybe that’s just legal-ese. (grin)
Auction participants would know all about option pricing, of course, and would apply a range of assumptions; presumably the sale would go to the buyer with the highest volatility assumption, which would probably (but not certainly) yield a higher price than Treasury got.
[Not sure how the author assesses this likelihood – or the extent to which his editorial biases are involved in the assertion. Nevertheless, it is possible that an auction-determined price might be higher, as a result of a “winner’s curse” problem. However, in all fairness, the winner’s curse says that the winner overpaid, so if the way that the Treasury can extract more is dependent on assuming they can find a schlub to overpay…]
The VIX index gives a good idea of the volatility of the market over time. Nevertheless, the volatility of the VIX or the XLF, the financial sector exchange traded fund, will understate the volatility of the typical stock in either index.
The average volatility of a stock in an index will be less than the index itself. This is because the stock returns are not perfectly positively correlated. When the components of an index have correlation coefficients less than one, the average stock will be more volatile than the whole portfolio of stocks. This is related to the idea of diversification in modern portfolio theory.
Unlike portfolio theory, the owner of a stock option has limited downside. Thus, volatility raises the value of options.
I meant to say that the average volatility of a stock in an index will be GREATER than the volatility of the index itself.